Logistic Regression¶

Logistic regression problem taken from: Sören Laue, Matthias Mitterreiter, and Joachim Giesen. “GENO–GENeric Optimization for Classical Machine Learning.” Advances in Neural Information Processing Systems 32 (2019). and https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression

Problem Description¶

Given a data matrix \(X\) of dimension \(n\times d\), and a label vector \(y\in\{-1,+1\}^n\).

We have the following unconstrained optimization problem,

\[\min_{w \in R^{d}} ||w||_1 + C \sum_{i=1}^n \log(\exp(-y_i(X_i^Tw))+1),\]

where \(C\) is the inverse of regularization parameter

Modules Importing¶

Import all necessary modules and add PyGRANSO src folder to system path.

[1]:

from time import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import l1_min_c
import sys
## Adding PyGRANSO directories. Should be modified by user
sys.path.append('/home/buyun/Documents/GitHub/PyGRANSO')
from pygranso.pygranso import pygranso
from pygranso.pygransoStruct import pygransoStruct
import torch

Data Initialization¶

Specify torch device, and generate data

Use GPU for this problem. If no cuda device available, please set device = torch.device(‘cpu’)

[2]:

device = torch.device('cuda')

iris = datasets.load_iris()
X = iris.data
y = iris.target

X = X[y != 2]
y = y[y != 2]

X /= X.max()  # Normalize X to speed-up convergence

# Demo path functions
cs = l1_min_c(X, y, loss="log") * np.logspace(0, 7, 16)

X = torch.from_numpy(X).to(device=device, dtype=torch.double)
y = torch.from_numpy(y).to(device=device, dtype=torch.double)
[n,d] = X.shape
y = y.unsqueeze(1)

Function Set-Up¶

Encode the optimization variables, and objective and constraint functions.

Note: please strictly follow the format of comb_fn, which will be used in the PyGRANSO main algortihm.

[3]:

# variables and corresponding dimensions.
var_in = {"w": [d,1]}


def user_fn(X_struct,X,y,C):
    w = X_struct.w

    f = torch.sum(torch.log(torch.exp(-y* (X@w)) + 1))
    f+= torch.norm(w,p=1)/C

    # inequality constraint
    ci = None

    # equality constraint
    ce = None

    return [f,ci,ce]

User Options¶

Specify user-defined options for PyGRANSO

[4]:

opts = pygransoStruct()
opts.torch_device = device
opts.maxit = 50
opts.opt_tol = 1e-6
np.random.seed(1)
opts.x0 = torch.zeros(d,1).to(device=device, dtype=torch.double)
opts.print_level = 0

Main Algorithm¶

[5]:

print("Computing regularization path ...")
start = time()
coefs_ = []
i = 0
for c in cs:
    i += 1
    comb_fn = lambda X_struct : user_fn(X_struct,X,y,c)
    torch.autograd.set_detect_anomaly(True)
    soln = pygranso(var_spec = var_in,combined_fn = comb_fn,user_opts = opts)
    print("Problem {} with C = {} completed".format(i,c))
    arr = soln.final.x.T.tolist()
    arr = np.array(arr).ravel()
    coefs_.append(arr)
print("This took %0.3fs" % (time() - start))

coefs_ = np.array(coefs_)
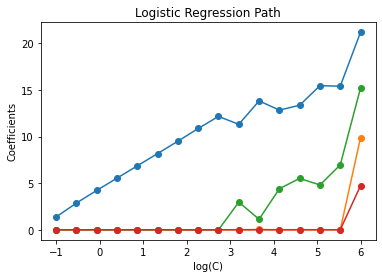
plt.plot(np.log10(cs), coefs_, marker="o")
ymin, ymax = plt.ylim()
plt.xlabel("log(C)")
plt.ylabel("Coefficients")
plt.title("Logistic Regression Path")
plt.axis("tight")
plt.show()

Computing regularization path ...
Problem 1 with C = 0.10007147962830593 completed
Problem 2 with C = 0.29307379488744323 completed
Problem 3 with C = 0.8583089764312021 completed
Problem 4 with C = 2.5136819185942896 completed
Problem 5 with C = 7.361680888087905 completed
Problem 6 with C = 21.55974671940413 completed
Problem 7 with C = 63.14083504447964 completed
Problem 8 with C = 184.917063358914 completed
Problem 9 with C = 541.5563525125441 completed
Problem 10 with C = 1586.0260682241312 completed
Problem 11 with C = 4644.906624058538 completed
Problem 12 with C = 13603.280537740799 completed
Problem 13 with C = 39839.17360792678 completed
Problem 14 with C = 116674.77924601595 completed
Problem 15 with C = 341698.95806769416 completed
Problem 16 with C = 1000714.7962830593 completed
This took 13.968s

../_images/examples_C3_logistic_regression_11_1.png

NCVX PyGRANSO Documentation